NIVELACIÓN POR RASANTE Y CURVAS DE NIVEL

 

Nivelación simple

Cota de BM= Elevación inicial + Vta. Atrás= Altura de aparato

Cota de BM= 700+ 1.370= 701.370

A la altura de aparato le iremos restando cada una de las vistas intermedias para ir obteniendo nuestras elevaciones, por ejemplo:

Elv 2A = 701.370- 1.330 = 700.040

Elv 3A = 701.370 – 1.340 = 700.030

Así iremos haciendo para ir obteniendo cada elevación ya que la altura de aparato será constante porque todos los puntos se pueden visualizar con una sola puesta de aparato.

 

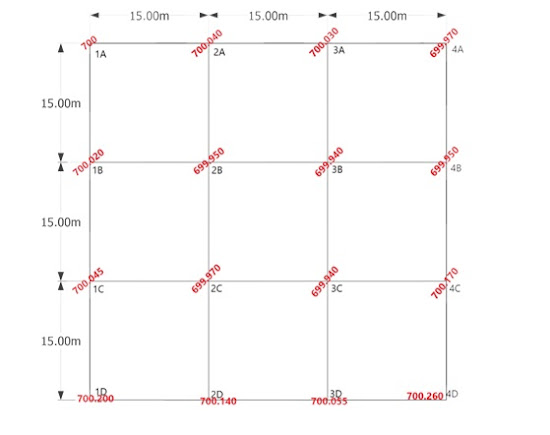
Para graficar las curvas de nivel.

Debemos fijarnos en que líneas pasara la curva de nivel.

 Como la curva la realizaremos a cada 0.50m solo pasaría la 700.000

Para determinar la distancia a la que pasara debemos hacerlo por el método de interpolación que no es más que formar 1 triangulo con la línea que analizaremos y aplicar una regla de tres de la siguiente manera:

Para las líneas diagonales sacaremos la raíz cuadrada de 15 al cuadrado más 15 al cuadrado para sacar la distancia de la diagonal lo cual da un resultado de 21.213m.

A continuación, analizaremos todos los triángulos necesarios para trazar nuestra curva de nivel.

 

 

Nivelación compuesta:

En el segundo caso utilizaremos la nivelación compuesta. Por lo tanto, el aparato se moverá más de 1 vez.

 

 Comprobación

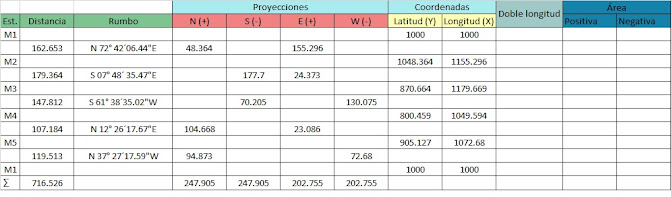
Para hacer la comprobación hacemos la sumatoria de nuestras vistas atrás y de nuestras vistas adelantes:

Σ V. atrás= 1.475 + 1.496 + 1.856 + 1.902= 6.729

Σ V. adelante= 1.350 + 1.400 + 1.230 + 1.110= 5.090

A nuestra Σ V. atrás le restamos la Σ V. adelante.

6.729-5.090= 1.639

Y a nuestra Elevación del punto final le restamos la elevación del punto inicial.

701.639-700= 1.639

Como ambas son iguales queda comprobado que el proceso de nivelación fue correcto.

Para comprobar el resultado: A nuestra sumatoria de lecturas de vista atrás le restaremos la sumatoria de vistas intermedias

5.381m – 3.142m = 2.239m

Y a nuestra elevación de llegada le restamos la elevación de salida.

102.239m – 100m= 2.239m

Como ambos resultados son iguales queda comprobado.

 

Como sabemos que la cuadricula está conformada por cuadros de 15 x 15 metros, debemos encontrar la distancia de una esquina a otra (línea roja), lo cual lo podemos hacer por medio de Pitágoras.

C2 = a2 +b2

C= √ a+b    

Entonces C= √ (15)2+(15)2 = 21.213m

 

Colocamos las elevaciones obtenidas en la tabla en la cuadricula.

 

 

Calculo de los puntos

Analizaremos cada cuadro de la cuadricula para ir determinando por donde pasan nuestras curvas de nivel que serán a cada 0.5 metros.

Fuentes:

Apuntes de clase Topografia I, Impartida por Ing. Raul Bermudez, Universidad de El Salvador, El Salvador, 2020